관련정보
Javier Marin Synthetic Tabular Data Generation
nbsynthetic 의 특징
- 심플하고 비지도 학습이다.
- 강건성: 모델 자체가 가볍기 때문에 계산 비용을 최소화하면서 학습 안정성을 보장하기 위해 특정 하이퍼 파라미터 튜닝을 적용
- For the experiments in this work we have use the python open source library nbsynthetic that uses a non-conditional Wassertein-GAN (논문인용)
Wassertein-GAN
[Limitation of GANs]

- Loss 자체가 판별자에서 생성된 loss 이기 때문에 뒤로 갈수록 구별을 잘 못하면서 수렴
- 하지만, 생성자는 성능이 계속 좋아짐 → 어디서 train을 멈춰야할지도 모른다. (학습이 불안정)
기존 GAN을 최소화하는 것은 JS-divergency를 최소화하는 것 같다.

- 확률 분포 p분포와 Q분포가 너무 다르면 gradient의 기울기가 거의 0이 나와 gradient vanishing 문제가 발생함→ 학습이 안됨
- 모드 붕괴: 특정 데이터, 특정 클래스만 계속 생성(생성자가 꼼수를 씀)
Wassertein-GAN 제안
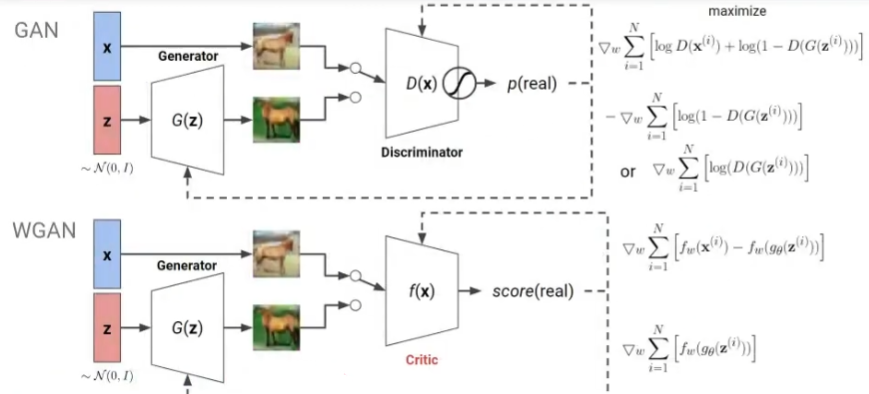
- Js divergence 대신 Wassertein distance(Earth Mover distance)
- 0~1 output 없앰→ 회귀처럼 -무한~+무한으로 예측
- clip이라는 방식 (-c,c) 하이퍼파라미터 c를 사용해서 Weight W를 자름

loss 처럼 수렴하면서 결과가 좋아지는 것이 보임
⇒ 더 연구가 필요하겠지만, 이러한 loss 함수의 특성으로 인해 device에서 생성되는 불규칙한 분포를 가진 데이터도 안정적이고 효과적으로 학습할 수 있는 것으로 보인다.
장점
- 감독되지 않는 아키텍처를 기반으로 하므로 사용자는 미리 정의된 대상이 필요하지 않음(비조건적)
- 연속형 특성과 범주형 특성을 모두 갖춘 소규모 데이터 세트를 대상으로 함(5000개 이하)
기존모델과 차이점
- 생성기와 판별기 모두에서 세개의 은닉층을 가진 Sequential 아키텍처를 사용함(G와 D가 연결된 순차적 아키텍처를 가지고 있음) → 심플함
- Learning rate (lr = 0.0002)로 사용 → 상당히 작음
- Reduced momentum term (or mean of the gradient) below the default value of 0.9 (β1 = 0.4)
- Wassertein distance(Earth Mover distance)라는 손실함수를 계산할 때 이 divergence를 사용
고찰
- 모델 구조가 심플하여 소규모 데이터 셋에 최적화 되어 있음
- lifelog 데이터 특성상 분포가 산발적(차이가 큰)으로 있기때문에 이러한 분포 특성상 Wassertein distance(Earth Mover distance) 쓰는게 안정적으로 학습한 것 같다.